Uncertainty Quantification in Node Classification
Why do we need to measure uncertainty?
Modern neural networks are widely applied in a variety of learning tasks due to their exceptional performance, but fail to express uncertainty about predictions. For example, if a neural network is trained to predict whether an image contains a cat or a dog and is given an elephant as input, it will not admit that it is unsure. With a relatively high probability the machine learning model will instead still choose cat or dog. For high-risk domains like healthcare and autonomous driving this is not the best approach. In these areas, the cost and damage caused by overconfident or underconfident predictions can be catastrophic.
Quantifying uncertainty of neural networks is also important for improving the transparency of the network itself. The NIST white paper on principles of explainable AI [1] defines the so-called, limits of knowledge principle this way: “A system only operates under conditions for which it was designed and when it reaches sufficient confidence in its output.” Clearly, the uncertainty of neural networks must be quantified accurately before they are used. Moreover, the inferred uncertainty can answer the user question: How accurate, precise and reliable are the predictions? Higher reliability will increase user trust in AI-driven systems and user acceptance of AI technologies. For more information about this, read the article “Questioning the AI: Informing Design Practices for Explainable AI User Experiences [2].”
Uncertainty in graph neural networks
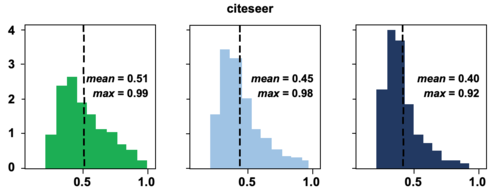
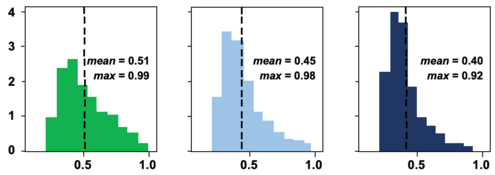
Modeling predictive uncertainty is critical for graph data. In node classification, the uncertainty is often represented as predictive probability (confidence) and computed with graph neural networks (GNNs). Figure 1 shows histograms of predictive probabilities learned with a graph convolutional neural network (GCNN) [3] for node classification in the citation network Citeseerx. Included are in-distribution (InDist) and out-of-distribution (OOD) nodes. The OOD nodes are nodes from classes of nodes not observed in the training data. Figure 1 shows that the statistics of the inferred predictive probabilities for different types of test nodes are similar. The middle panels reveal that the GNN method is confident of its false predictions. The right panels show a similar tendency for the OOD case. Though the GNN does not learn any knowledge in terms of the OOD nodes (which represent unobserved classes), it still classifies them along with the observed classes with high confidence. From the example, it is clear that for the node classification a more sophisticated method is required to model predictive uncertainty with any accuracy.
Modeling uncertainty
If the predictive probabilities stated do not necessarily match the real uncertainty (as shown in Figure 1), then the question naturally arises: How can we appropriately quantify predictive uncertainty for node classification?
To solve this, we propose the novel method, Bayesian Uncertainty Propagation (BUP). Based on Bayesian confidence, this method quantifies the uncertainty of the prediction through modeling distribution of the predictive probability. In particular, we model the message θi ∈ RC, one for each node i that represents latent features of the node, as a random variable following a distribution p(θi|X,A). In Bayesian framework, θi is known as unobservable variables introduced as part of the models that are to be learned from the data. Multiple values of the message could be consistent with the observations. Thus it is reasonable to model its randomness, i.e., the distribution of the message, rather than a fixed value. As the message θi is a continuous variable, we assume it follows a Gaussian distribution with mean function mi = g(X, A; γ) and covariance function Σi = h(X, A; ψ). The two functions are defined with GNNs, as neural networks are good function approximators, especially for complicated data. By modeling message uncertainty, we can then estimate the distribution of the predictive probability p(yi|θi). The larger the variance Σi, the larger the Bayesian confidence interval of the predicted probability, resulting in a more uncertain prediction. Since the message θi is multidimensional, we can use the averaged variance or the Gaussian entropy to quantify the predictive uncertainty.
Uncertainty propagation between nodes
The Gaussian distribution of the message is fully characterized by the mean function mi and the covariance function Σi. As both functions are approximated with neural networks the question is: How we can define the two neural networks reasonably? A straightforward idea could be: constructing two GCNNs with the same architecture but different parameters for mean and covariance. However, GCNN’s message-passing mechanism does not work well for the covariance function Σi. Intuitively, if a node i is connected with multiple nodes, we can reasonably estimate that the prediction uncertainty of the node should be smaller than that of another node j, which has fewer links, since the prediction of the node i will be conditioned on more evidence. The intuition cannot be matched with the popular message-passing mechanism, e.g., GCNN, where there is no guarantee that linking to more neighbors leads to less uncertainty. Thus, we introduce a novel propagation mechanism, inspired by Gaussian process, to pass uncertainty between nodes. Particularly, we compute conditional Gaussian of a message θi given its neighbors. With the novel passing mechanism, the more neighbors the node i links, the more the uncertainty is reduced by the available evidence, resulting in smaller variance of the node.
Validation and summary
In this work, we demonstrate the effectiveness of BUP using popular benchmark datasets and analyze the learned uncertainty in depth. The key findings of the research are:
- This work achieves more reliable (well-calibrated) results, which means the inferred predictive probability of our method is closer to the true one.
- The predictions of the proposed method present the uncertainty accurately in the OOD setting.
- The uncertainty of the OOD nodes is significantly larger than that of in-distribution ones.
- The proposed method captures the influence of the graph structure on the uncertainty of the predictions. For example, the nodes with more neighbors report less uncertainty on average.
Uncertainty estimation is an important task in achieving transparency of GNNs and was created to learn the knowledge limit of these methods. The proposed approach explicitly quantifies uncertainty in node classification with Bayesian confidence of predictive probability. Beyond the deterministic process of most GNNs, the proposed method models the uncertainty of the messages and captures how the uncertainty propagates over the graph, by which the distribution of the predictive probability can be learned in an elegant manner.
The work is detailed in the research paper “Uncertainty Propagation in Node Classification” [4] and was written by Zhao Xu, Carolin Lawrence, Ammar Shaker, Raman Siarheyeu. It was and presented at the 22nd IEEE International Conference on Data Mining.
Dr. Zhao Xu
References
1. P. Jonathon Phillips, Carina Hahn, Peter Fontana, Amy Yates, Kristen Greene, David Broniatowski, and Mark Przybocki. Four principles of explainable artificial intelligence. NIST Interagency/Internal Report (NISTIR), National Institute of Standards and Technology, Gaithersburg, MD, [online], 2021.
2. Q. Vera Liao, Daniel Gruen, and Sarah Miller. Questioning the AI: Informing design practices for explainable AI user experiences. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems. Association for Computing Machinery, 2020.
3. Thomas Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations. Toulon, France, 2017.
4. Zhao Xu, Carolin Lawrence, Ammar Shaker, and Raman Siarheyeu. Uncertainty propagation in node classification. In Proceedings of the IEEE International Conference on Data Mining. Orlando, USA, 2022.