A Study on Ensemble Learning for Time Series Forecasting and the Need for Meta-Learning
Time series forecasting estimates how a sequence of observations continues into the future. It overcomes the current limitations of predictive modeling when incorporating temporal dependencies of time series data, and has the potential to be widely applied in areas such as resource forecasting (e.g., forecasting peak electricity or cellular service demands), financial modeling and predicting the spread of pandemics.
One of the crucial decisions for prediction performance is selecting a forecasting algorithm, referred to as the base method or algorithm. Using an ensemble method (also called an ensemble algorithm or simply ensemble), different base algorithm predictions can be combined to improve a base method’s performance for a given dataset. There is a plethora of base and ensemble algorithms available.
In this blog post, we discuss the performance of ensemble methods for time series forecasting. We obtained our insights from conducting an experiment that compared a collection of 12 ensemble methods for time series forecasting, their hyperparameters and the different strategies used to select forecasting models. Furthermore, we will describe our developed meta-learning approach that automatically selects a subset of these ensemble methods (plus their hyperparameter configurations) to run for any given time series dataset. The information in this blog post is taken from the research paper titled, “A study on Ensemble Learning for Time Series Forecasting and the need for Meta-Learning (Julia Gastinger et al.)” and was presented at the 2021 International Joint Conference on Neural Networks (IJNN 2021).
Lowering the Workload of Data Scientists with Automated Time Series Forecasting
Automated time series forecasting lowers the workload of data scientists by automating the selection of base methods, ensemble methods and associated hyperparameters for a given time series dataset. Data scientists usually carry out these steps manually. It provides a structured approach to identifying well-performing base algorithms, ensemble algorithms and hyperparameter configurations for a given time series dataset.
At NEC Laboratories Europe, we have developed a platform for automated time series forecasting called HAMLET. The platform leverages forecasting algorithms for any given time series dataset and combines algorithm predictions with promising ensemble method(s).
Ensemble Learning for Forecasting
Ensemble methods seek better predictive performance by combining predictions from multiple base models. We collected and implemented a wide range of ensemble methods (with and without exogenous variables) to assess their effectiveness for time series forecasting. An explanation of base algorithms and ensemble methods can be seen in the figure below.
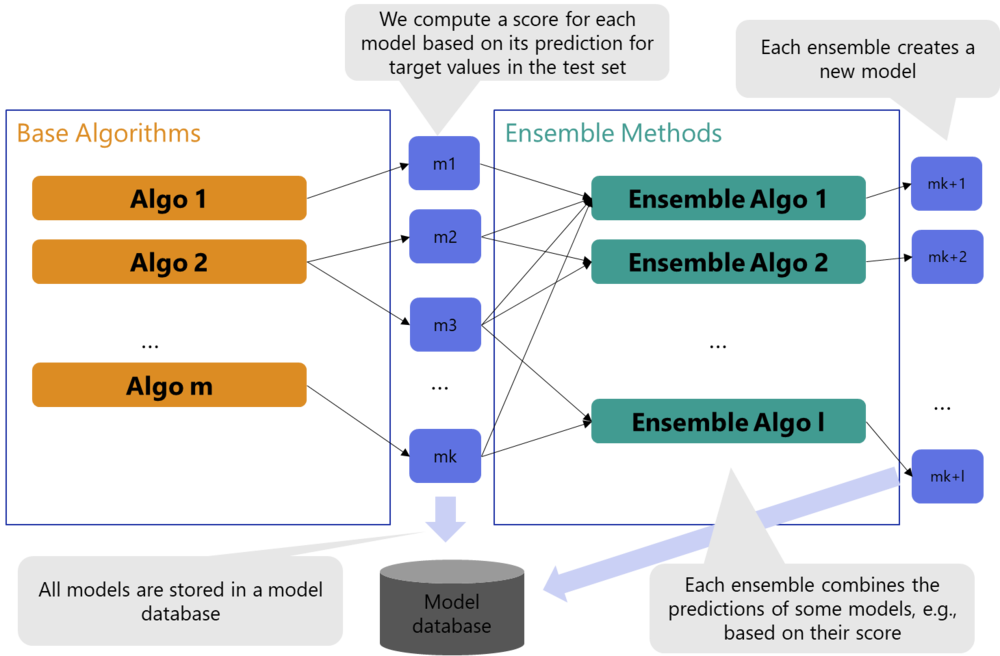
Figure: Base Algorithms and Ensemble Methods – an Explanation
The figure illustrates the base algorithms Algo 1 until Algo m, where Algo is short for algorithm, and m is the number of implemented algorithms shown in orange boxes. Each algorithm produces one or multiple forecasting models represented by blue boxes. In total, the base algorithms produce k models: m1,…,mk. In addition, green boxes show the Ensemble Algorithms: Ensemble Algo 1,…, Ensemble Algo l. Each ensemble algorithm creates a new model. We denominate the models created by the ensemble algorithms with mk+1,…,mk+l. All models are stored in a model database.
Collected ensemble methods vary depending on the meta-models used, strategies chosen to select the models, way of computing combination weights and integration of exogenous variables. We implemented different selection strategies to select which, and how many, base models the ensemble methods combine. Details about these topics are described in the previously mentioned research paper, “A study on Ensemble Learning for Time Series Forecasting and the need for Meta-Learning.”
We conducted an experiment on approximately 16000 time series datasets from the renowned forecasting competitions M3, M4, M5, and an economic database. The experiment was designed to answer the following research questions:
- Do ensemble methods help to improve forecasting accuracy?
- With the goal of reaching the best possible forecasting accuracy for automated domain-agnostic Time Series Forecasting, and the possibility to run multiple ensemble methods in parallel: Which ensemble methods (including hyperparameter configurations) should be selected?
- Do the results differ significantly for different dataset-sources (the different M competitions and the economic database)?
In the experiment, we found that ensemble methods improve overall forecasting accuracy, with simple ensemble methods providing good results on average. However, different ensemble methods are suited to different time series datasets. This makes it challenging to preselect one or multiple ensemble methods for a given time series dataset that return a high level of accuracy.
To overcome this, we propose using a meta-learning approach designed to preselect one or more ensemble methods for each new time series and their hyperparameter setting (based on the dataset’s meta-features).
Meta-Learning for Ensemble Selection
The proposed meta-learning method, which we refer to as the meta-learner, is able to choose a promising subset of ensemble methods plus hyperparameter configurations (ensemble +HP) to be used for a given dataset. The selection is determined by the dataset’s meta-features.
Meta-features describe the properties of the dataset, for example, the number of samples or spectral entropy. We fit one classifier for each ensemble+HP. To create the dataset for meta-learning, we use the performance of ensemble+HP obtained from our experiment with ~16000 datasets. Each meta-learning dataset sample describes one time series. The features of the meta-learning dataset are the meta-features of the respective time series. The target value is binary, being 1 (select), or 0 (do not select).
We tested the meta-learner with 1632 datasets that were previously unknown to it, and compared the results to two baselines: autorank-based selection and random selection. For each dataset, autorank-based selection selects the ensemble+HPs that ranked best in the above described experiment. For each dataset, random selection selects a random set of ensemble+HPs. Our objective of this test was to answer the following research questions:
- Does the meta-learner improve the selection process compared to baseline methods?
- Did we select valuable meta-features for training the meta-learner?
We can show that the meta-learner outperforms the two baselines, and we are confident that these results can be further improved. For more information on the meta-learner, test setup and detailed results refer to the paper “A study on Ensemble Learning for Time Series Forecasting and the need for Meta-Learning.”
Conclusion
Ensemble methods improve the accuracy of time series forecasting. Our experiment with ~16000 datasets demonstrates this by analyzing the performance of ensemble methods on a large number of datasets from various domains. We further introduced a meta-leaning method that enables us to preselect ensemble methods for each new time series dataset (based on the dataset’s meta-features).
HAMLET, our platform for automated time series forecasting, will reduce the large number of manual tasks carried out by data scientists for this activity. It automates important decision steps for data scientists while, at the same time, making time series forecasting more accessible for non-experts.
Our continuing research ensures that ensemble methods integrated into HAMLET will improve the accuracy of domain-agnostic time series forecasting when compared to using base methods. By using the meta-learning method, we can save computing resources: the platform does not need to run all ensemble methods (plus hyperparameter configurations), while still reaching high accuracy compared to baseline selection methods. If you would like to learn more about ensemble methods, you can read our previous post “Metabags: Bagged Meta-Decision Trees for Regression” that discusses learning of heterogeneous regression ensembles.